🤖 모델 적합도(Model Fit)와 편향(Bias) · 분산(Variance)

1. 모델 적합도(Model Fit)

머신러닝 모델이 제대로 동작하지 않을 때는 모델의 적합도(Fit) 를 살펴봐야 합니다.
모델이 데이터를 얼마나 잘 설명하는지가 핵심입니다.

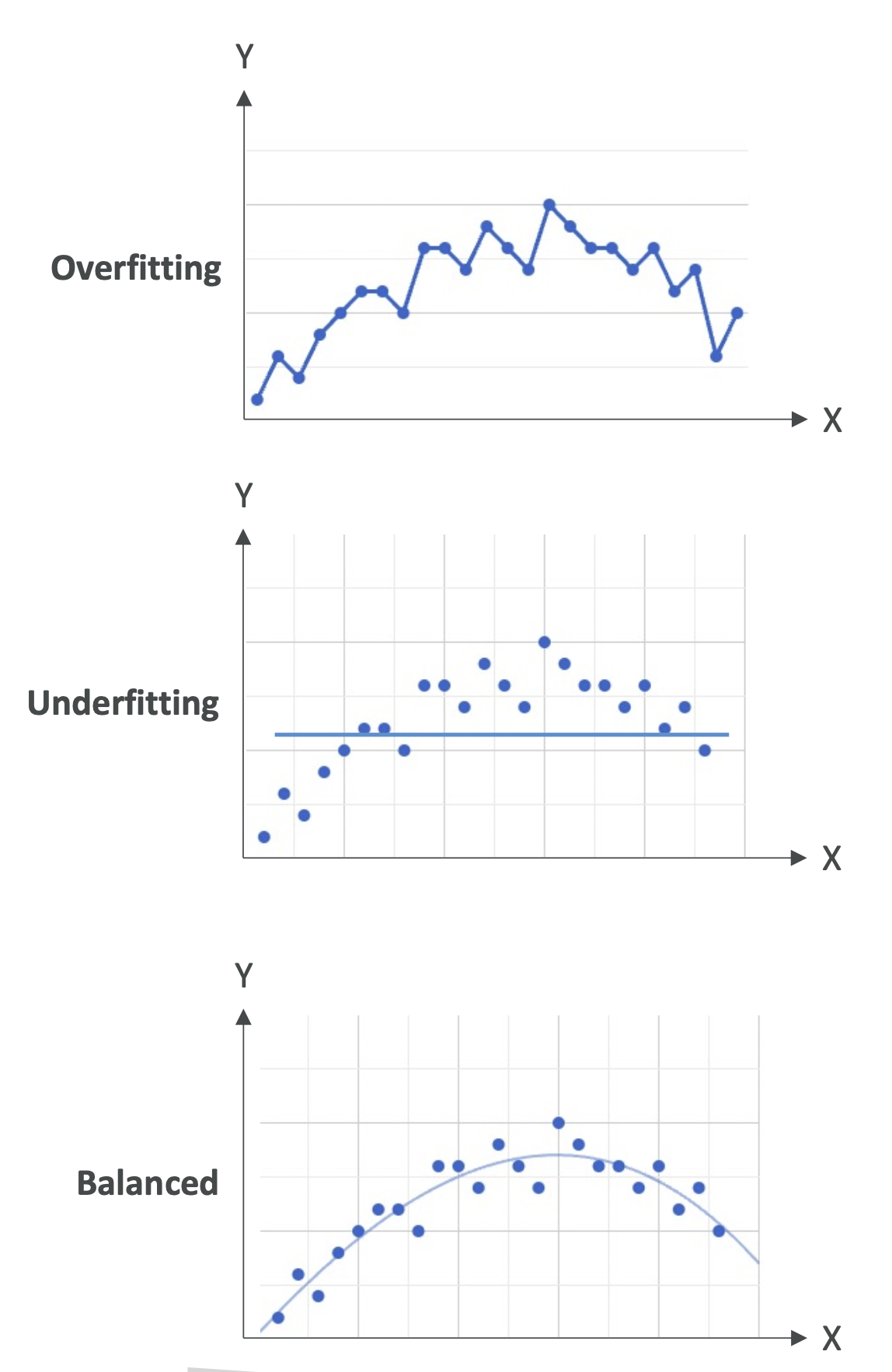
  • 과적합(Overfitting)

    • 훈련 데이터에서는 성능이 매우 좋음
    • 새로운 데이터(검증/테스트 데이터)에서는 성능이 나쁨
    • 원인: 모델이 데이터의 노이즈까지 학습해서 일반화가 안 됨
    • 📌 예시: 훈련 데이터 점 하나하나에 맞게 선을 구부려 만든 복잡한 곡선

  • 과소적합(Underfitting)

    • 훈련 데이터에서도 성능이 나쁨
    • 원인: 모델이 너무 단순하거나, 특징(Feature)이 부족함
    • 📌 예시: 복잡한 곡선 데이터에 단순 직선을 억지로 적용

  • 균형(Balanced)

    • 과적합도, 과소적합도 아닌 상태
    • 어느 정도 오차는 있지만, 데이터의 전체적인 패턴을 잘 따름
    • 📌 가장 이상적인 상황

2. 편향(Bias)과 분산(Variance)

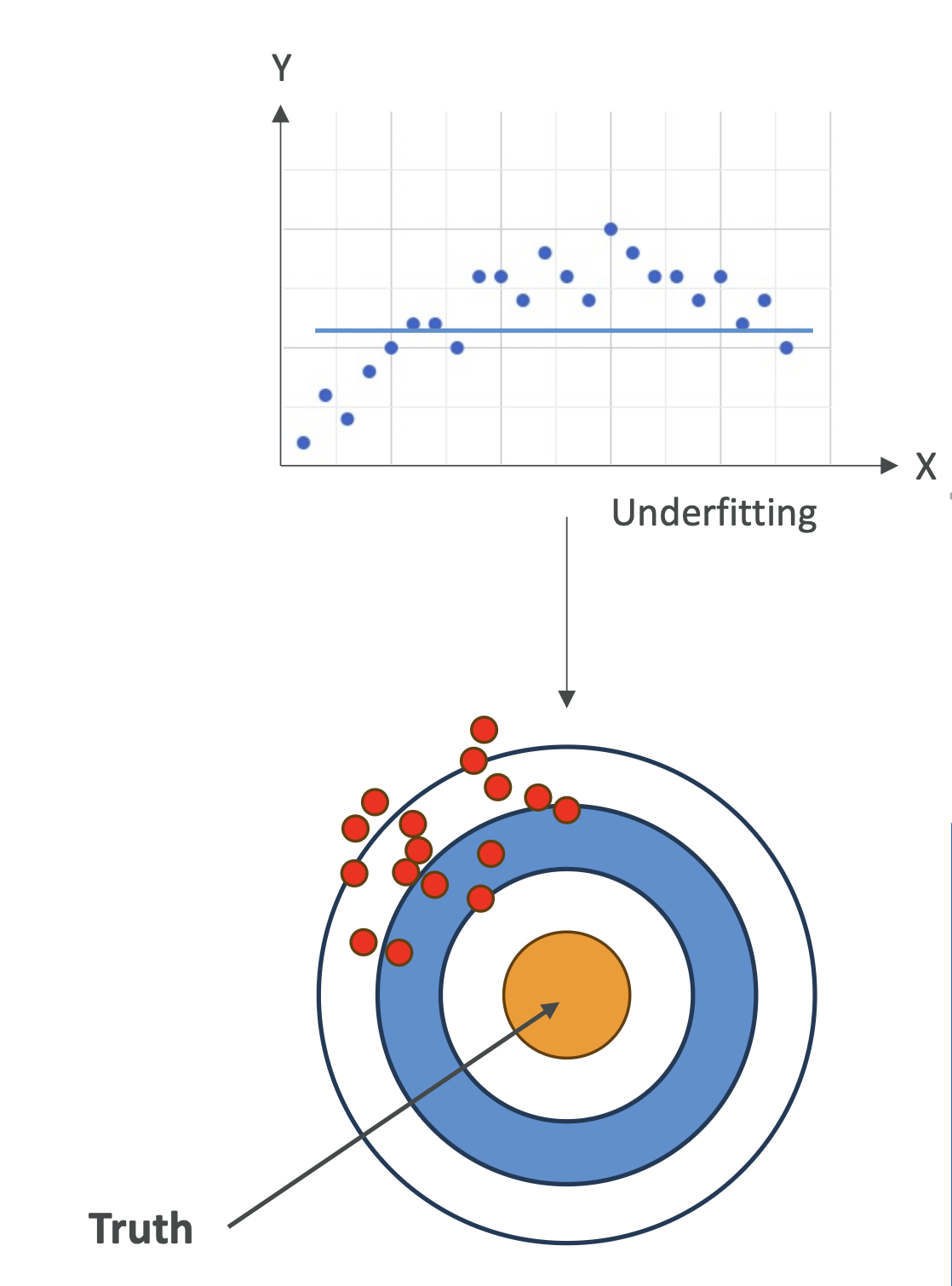
📌 Bias (편향)

  • 정의: 실제 값과 예측 값의 차이
  • High Bias (편향 높음)
    • 모델이 데이터 패턴을 잘 잡지 못함 → 과소적합
    • 예시: 곡선 패턴 데이터를 직선으로 예측
  • 줄이는 방법
    • 더 복잡한 모델 사용 (예: 선형 → 비선형 모델)
    • 더 많은 특징(Feature) 추가

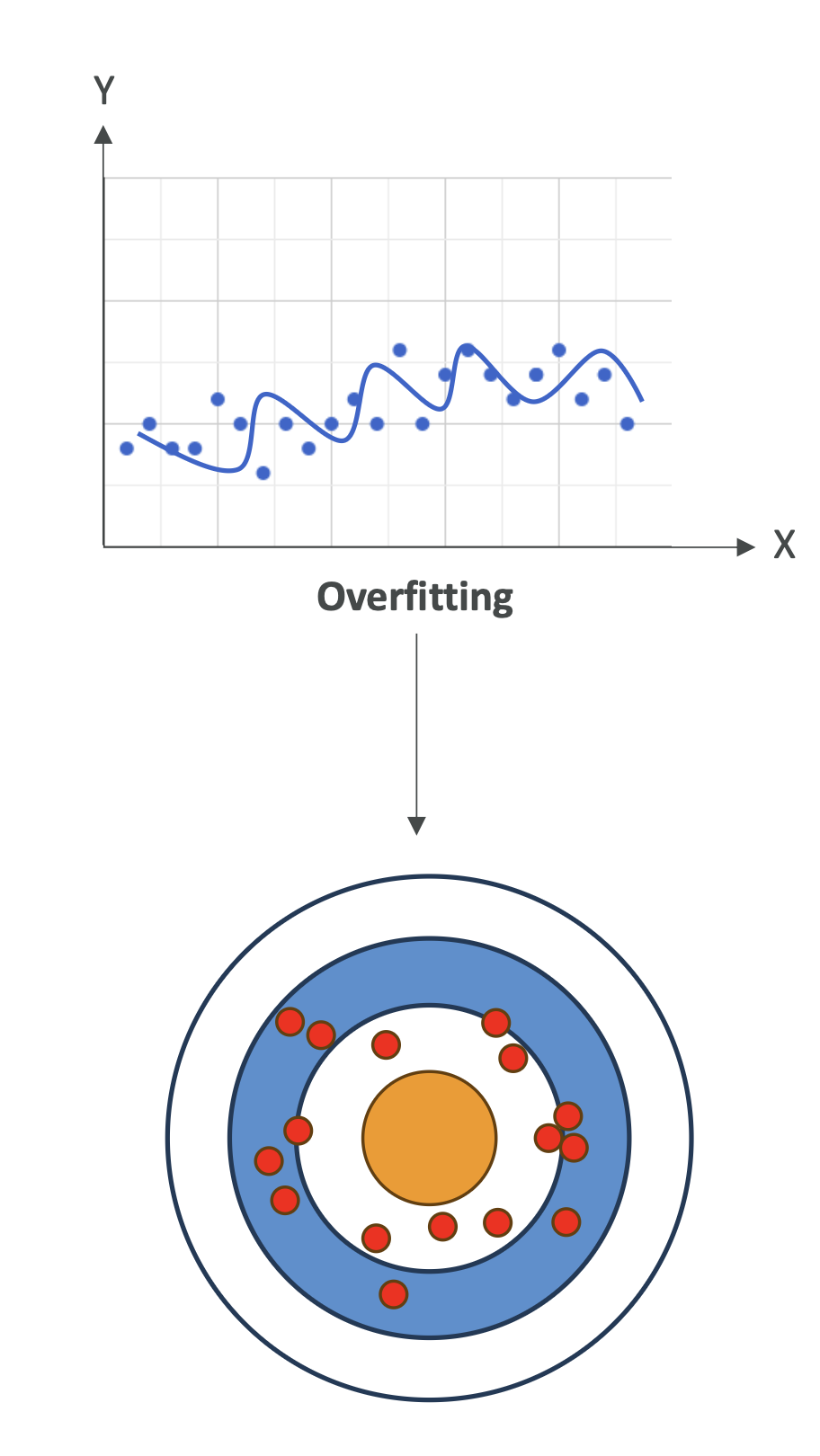
📌 Variance (분산)

  • 정의: 훈련 데이터를 조금만 바꿔도 모델 성능이 크게 달라지는 정도
  • High Variance (분산 높음)
    • 훈련 데이터에서는 성능이 매우 좋지만, 새로운 데이터에서는 성능이 급격히 떨어짐
    • 즉, 과적합 상황
  • 줄이는 방법
    • 불필요한 특징 제거 (Feature Selection)
    • 데이터셋을 여러 번 나눠서 교차검증(Cross Validation) 수행
    • 정규화(Regularization, 예: L1/L2) 적용

3. Bias-Variance Tradeoff (편향-분산 트레이드오프)

머신러닝에서는 Bias(편향) 과 Variance(분산) 사이에서 균형을 맞추는 것이 중요합니다.

  • High Bias + Low Variance → 과소적합
  • Low Bias + High Variance → 과적합
  • Low Bias + Low Variance → 이상적인 모델
  • High Bias + High Variance → 최악의 경우 (피해야 함)

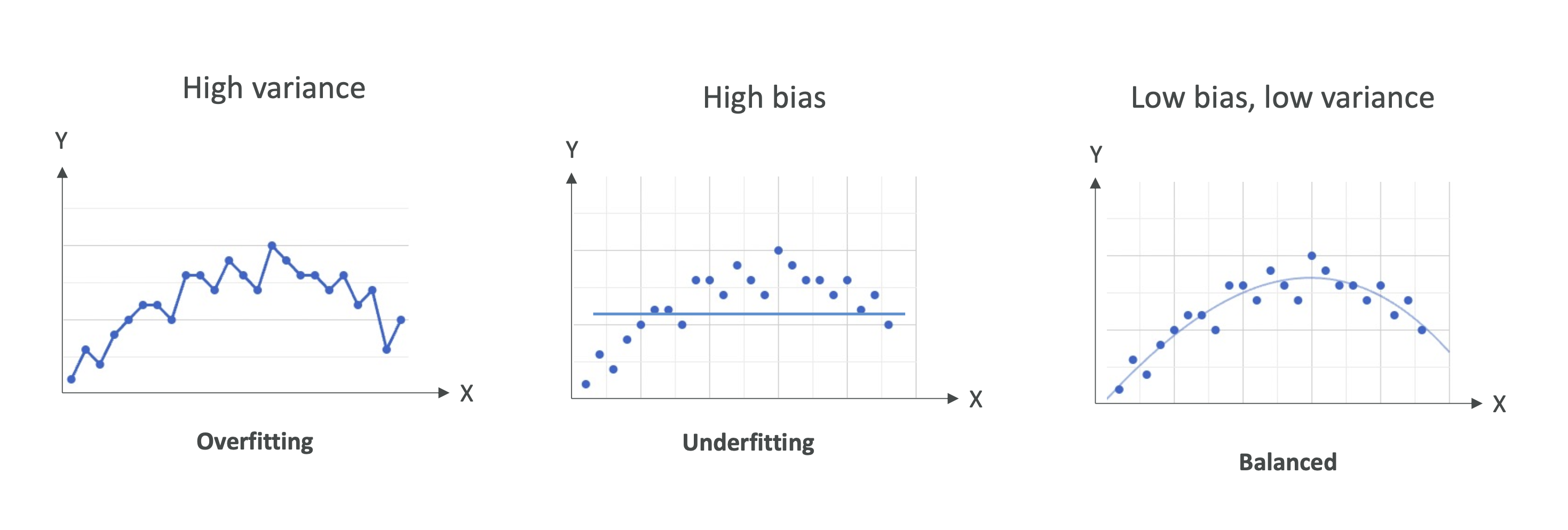
📌 시험 포인트:

  • 과적합 ↔ 분산 높음 (Variance High)
  • 과소적합 ↔ 편향 높음 (Bias High)
  • 균형 잡힌 모델이 가장 좋은 상태

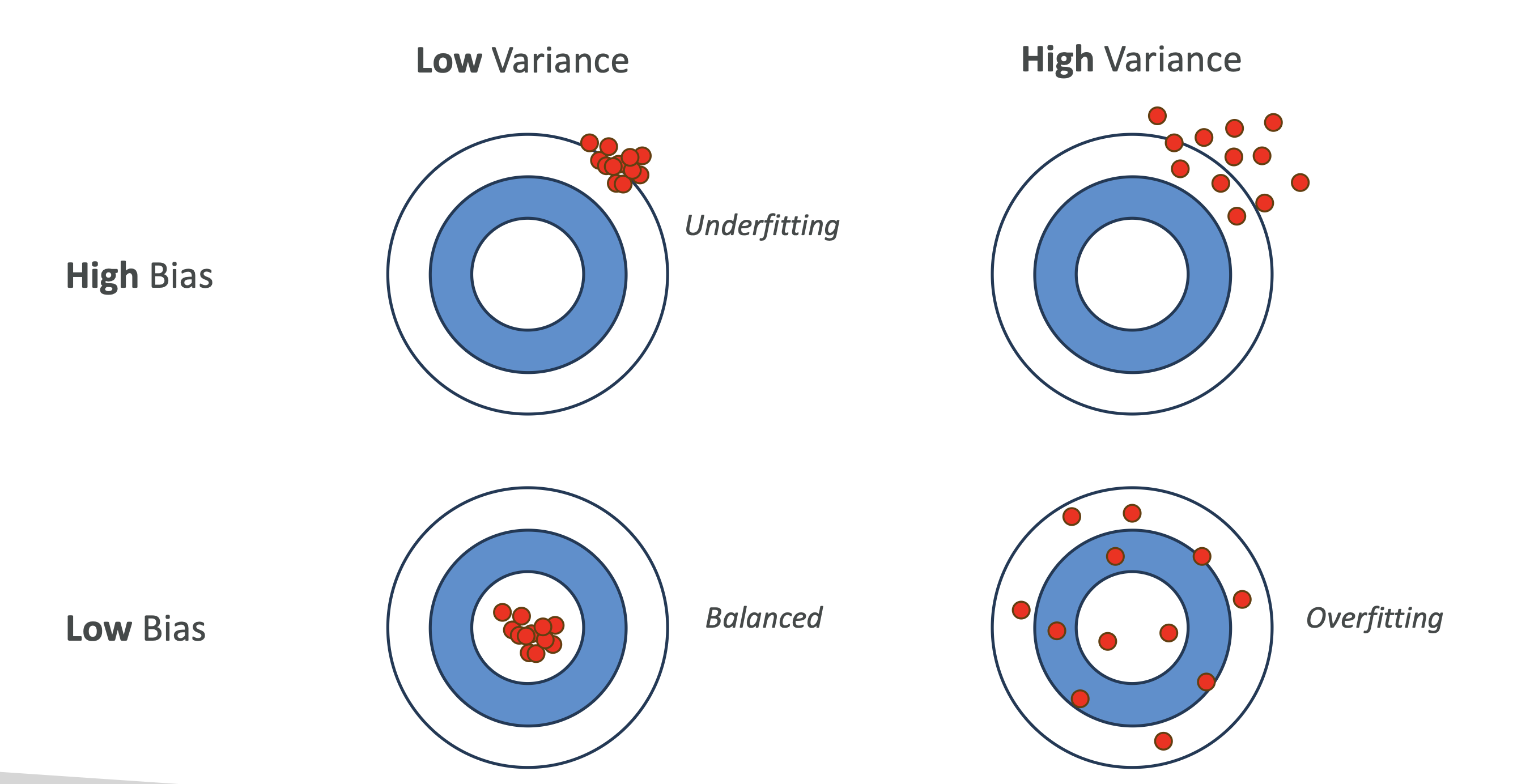
4. 시각적 이해 (다트판 예시 🎯)

  • 편향(Bias): 다트가 과녁의 중심에서 얼마나 떨어져 있는지
  • 분산(Variance): 다트가 흩어져 있는 정도
구분 설명 결과
High Bias + Low Variance 계속 같은 위치에 맞추지만 중심에서 멂 Underfitting
Low Bias + High Variance 중심 근처에 맞추지만 흩어져 있음 Overfitting
Low Bias + Low Variance 중심에 가깝고 모여 있음 Best Model
High Bias + High Variance 멀리 있고 흩어져 있음 Worst Model

✅ 시험 대비 Key Takeaways

  1. Overfitting → 훈련 데이터 잘 맞춤, 테스트 데이터 성능 나쁨 → Variance ↑
  2. Underfitting → 훈련 데이터조차 성능 나쁨 → Bias ↑
  3. Balanced Fit → Bias와 Variance 모두 낮아야 함
  4. Bias-Variance Tradeoff 개념 숙지 필수
  5. AWS 자격증 시험에서는 과적합 / 과소적합을 어떻게 해결할지를 물을 수 있음
    • 과적합 해결: Regularization, Feature Selection, Cross Validation
    • 과소적합 해결: 더 복잡한 모델, Feature 추가

  • 편향은 실제 문제(복잡할 수 있음)를 더 단순한 모델로 근사할 때 발생하는 오류입니다. 편향이 높으면 모델이 특성과 목표 출력 간의 관련 관계를 놓치게 되어 과소적합(underfitting)이 발생할 수 있습니다.

  • 분산은 모델이 학습 데이터의 작은 변동에 민감하게 반응하여 발생하는 오류입니다. 분산이 높으면 모델이 의도한 출력 대신 학습 데이터의 무작위 잡음을 모방할 수 있습니다(과적합).

  • 편향과 분산을 모두 증가시킬 수 있지만, 그렇게 하면 일반적으로 모델이 과소적합과 과대적합을 모두 겪게 되어 성능이 저하됩니다. 편향이 높으면 모델이 중요한 패턴을 놓치게 되고(과소적합), 분산이 높으면 모델이 훈련 데이터의 노이즈에 지나치게 민감해집니다(과대적합).

  • 예를 들어, 학습 데이터의 양을 줄이면 모델이 학습할 수 있는 정보가 줄어듭니다. 이는 모델이 기본 패턴을 제대로 포착하지 못하여 편향(과소적합)을 증가시킬 수 있습니다. 동시에, 데이터가 줄어들면 모델이 학습 데이터의 변동에 더 민감해져 분산이 증가할 수 있습니다.